Quick Review:
Real numbers have real-world values like dollar amounts, weights,
distances, age, temperature, and so on.
Rational numbers are real integers and fractions, and relate to
the "ratio". Rational numbers can be written as a ratio,
or quotient, of two integers.
Ex: The fraction ½ is the ratio of 1 to 2.
Ex: Three can be expressed as 3/1, which is a ratio of 3:1.
Ex: Since 0.57 can be written as the fraction 57/100, it is a rational number.
Irrational numbers are real numbers that can't be expressed as a quotient of two integers, such as non-repeating
and non-terminating numbers. To calculate the area
of a circle, a non-repeating, non-terminating irrational number is used, which has a symbol all it's own:
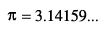
Coefficients are the number alongside the variables (which are
letters that represent mysterious numberous). In 3x2 + 2y + 7xy + 5, the 3 is
the coefficient of the first term. The 2 is the coefficient of the second term, and the 7 is the coefficient of the third
term. The 5 is the *constant*, because it doesn't have a mysterious *variable* that can change the value.
Equations are mathematical expressions that contain an equals sign.
Inequality symbols are used when you don't know what the expression equals:
> greater than
< less than
<
less than or equal to
> greater than or equal to
Properties of numbers are commutative (addition and multiplication
can be done in any order), associative (addition and multiplication can be done in any choice
of groupings), and distributive (terms multiplied by terms in parenthesis, must be "distributed" across all
the terms inside the parenthesis:
2x(5 + y) = 10x + 2xy
Density (decimal numbers can be made more exact), and identity (zero added to any number equals the
number).
Exponents: 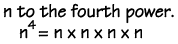
Any number raised to the zero power (except
0) equals 1.
Any number raised to the power of one equals itself.
To multiply terms with the same base, add the
exponents.
To divide terms with the same base, subtract the
exponents.
When a product has an exponent, each factor is
raised to that power.
A number with a negative exponent equals its reciprocal
with a positive exponent.
Rules of 1 - Any number raised to the power of "one" equals itself. This makes sense, because the power
shows how many times the base is multiplied by itself. If it's only multiplied one time, then it's logical that it equals
itself.
One raised to any power is one, because one times one times
one, as many times as you multiply it, is always equal to one.
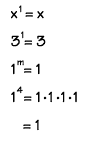
Product Rule - The exponent "product rule" tells us that, when multiplying two powers that have the same base,
you can add the exponents. In this example, you can see how it works. Adding the exponents is just a short cut!
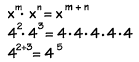
Power Rule - To raise a power to a power, multiply the exponents. Here you see that 52 raised
to the 3rd power is equal to 56.
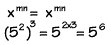
Quotient Rule - We can divide two powers with the same base by subtracting the exponents. You can see
why this works if you study the example shown.
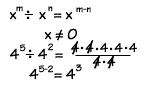
Zero Rule - Any nonzero number raised to the power of zero equals 1.
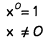
Negative Exponents - Any nonzero number raised to a negative power equals its reciprocal raised to the opposite
positive power.
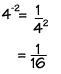
Be careful when combining!
Terms like x2yz
and xy2z look a lot alike, but they aren't and cannot be combined. Write the terms carefully when working
out problems.
Don't overlook terms that are alike!
Terms obey the associative property of multiplication
- that is, xy and yx are like terms, as are xy2 and y2x.
SIMPLIFYING - Whenever a problem can be simplified,
you should simplify it before substituting numbers for the letters. This will make your job a lot easier! To simplify an algebraic
expression:
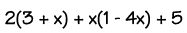
- Clear the parentheses.
- Combine like terms by adding coefficients.
- Combine the constants.
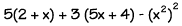
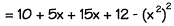
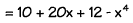
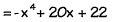

The continental United States - the lower 48 states
- has about 16,900 miles of shoreline. This is about ½ the length of the shoreline of Alaska. About how many miles of shoreline
does Alaska have?
We can write a division equation to find the answer to problems
like this. Our unknown number is the length of shoreline in Alaska. Let x represent this number. We know that x divided by
2 is the approximate length of shoreline in the lower 48 states. We can write the equation like this:
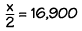
To solve this equation, we can use the inverse of dividing by
2, or multiplying by 2. If we multiply the left side of the equation by 2, we will get x alone on the left. Remember, any
operation done to one side must also be done to the other side, so we must also multiply the right side by 2.
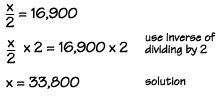
We multiply, and find that x, the length of the shoreline of
Alaska, is equal to 33,800 miles.
To check our answer, we substitute the value of 33,800 into
the original equation, like this.
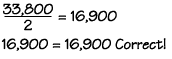
F=9/5C+32 calculates farenheit to celsius
Distance = Rate x Time
********
x axis is on the horizontal
y axis is on the vertical
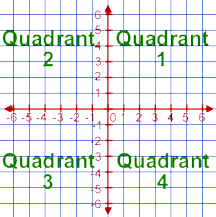
The coordinate plane . Slope and y-intercept. Graphing linear equations.
Graphing Equations and Inequalities
The above section created with the assistance of math.com

